In a grade one Waldorf classroom, the day commences with an engaging activity involving bean bags. Students gather in a circle, each holding a bean bag, and begin counting in rhythm. The teacher initiates the counting, and the children respond, creating a harmonious classroom chorus while passing the bean bags among themselves. This method of incorporating movement not only makes mathematics more interactive but also facilitates a deeper understanding of the subject compared to traditional rote textbook methods.
Dr. Hiten Lad, a neuropsychologist and parent within the Waldorf community, explains that this dynamic approach “stimulates the brain in its entirety.” By infusing movement into math lessons, students internalize mathematical concepts more profoundly, enhancing retention and comprehension. This exemplifies the essence of Waldorf Education, where mathematics intertwines with art, imagination, history, and writing, resulting in an unparalleled immersive learning experience.
In grade one the child is able to imagine or think in pictures, which is the foundation stone for learning.


In the early years of Grade 1 and 2, students discover the ubiquity of numbers in the world, even in nature. They foster the enjoyment of mathematics through use of games and puzzles. They develop greater facility with mental arithmetic and also the sense of importance of form and organization in the written practice of math problems.
By Grade 3, they delve into measurements and calendar mathematics as it becomes quite practical. Telling time, making change with money, measurement in cooking or in building all have their place. For the Grade 3 students’ math is very much a tool for dealing with life.



Fractional understanding becomes the focus in Grade 4. The study of fractions is introduced with physical (and yummy) objects to experience math in a concrete way before forming mental concepts. We begin with the concept of a whole, the world, you, me or a cake.

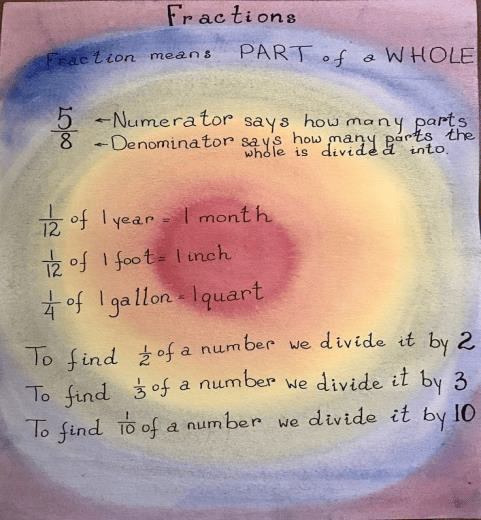

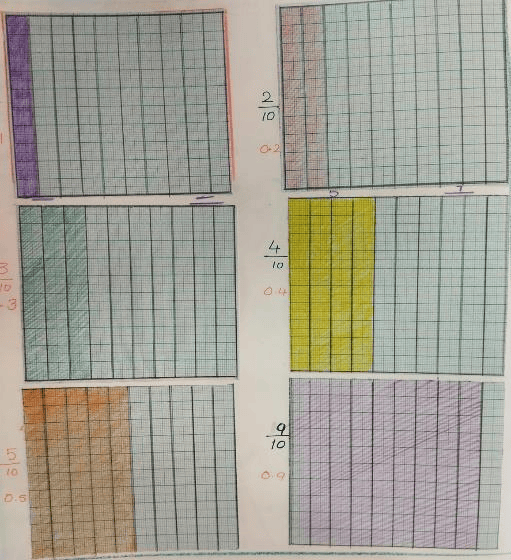
In grade 5 more complex fractions studies, multiplying and dividing mixed fractions and mixing the four operations in a problem are introduced to square, prime and abundant numbers. Decimals are introduced and students learn how to use all four operations with decimal fractions, followed by learning to convert fractions to decimals and vice versa. All these makes a great foundation for later work. Freehand geometry is also brought to the fifth grade students.

Teaching changes significantly in the sixth grade to address new conceptual capacities that are awakening in the children of their age therefore Business math takes the spotlight in Grade 6. The sixth grade is a firm, intentional step into the outer world.

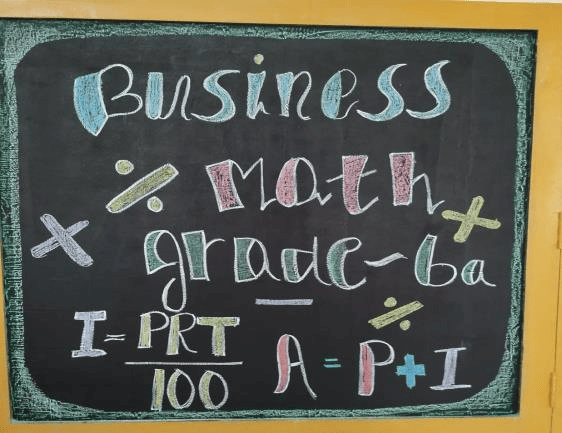
Students learn the interest rate formula in business math as a beginning to algebra studies. Geometry is taught as a separate main lesson block. Students learn to use the tools of geometry: a compass, ruler, and protractor. They draw various geometric constructions and learn to bisect lines and angles. Various geometric proofs are introduced in the sixth grade as a means to prepare the students for a more in-depth study of theoretical geometry in seventh grade.
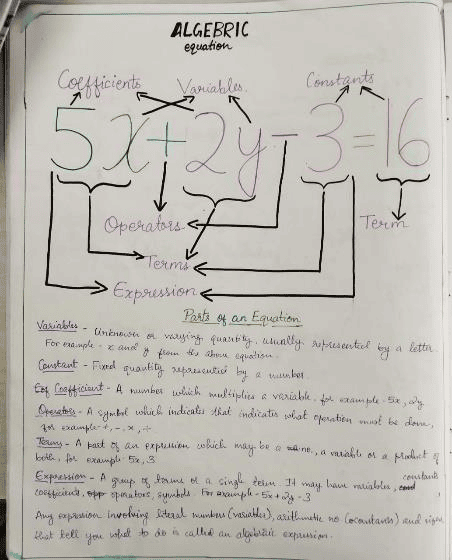

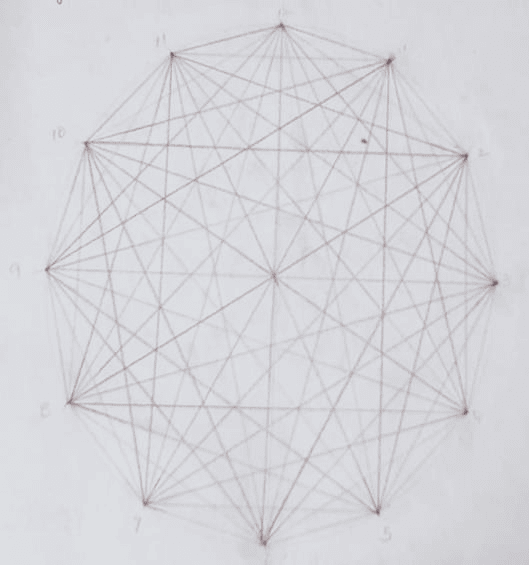
In Grade 7 the students are focused both out into the world that they are moving quickly towards and on themselves and their growing and deepening emotional and intellectual inner life. This requires a curriculum that echoes the energy of the seventh grader. With the study of algebra, the students are introduced to abstract mathematical thinking for the first time, freed of its relationship to computation. In geometry, the class moves into the computation of areas of polygons and solids. More divisions of the circle are drawn and students learn the possible transformations arising out of nested forms as an introduction to the spiral forms. Computing pi and deriving the formula for area and circumference of the circle are included.

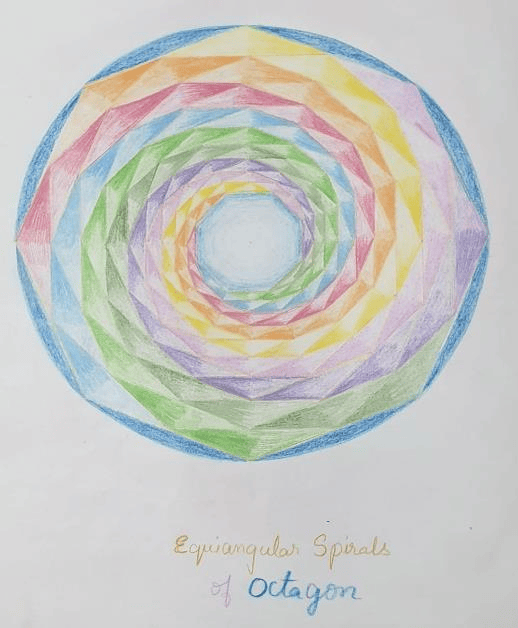
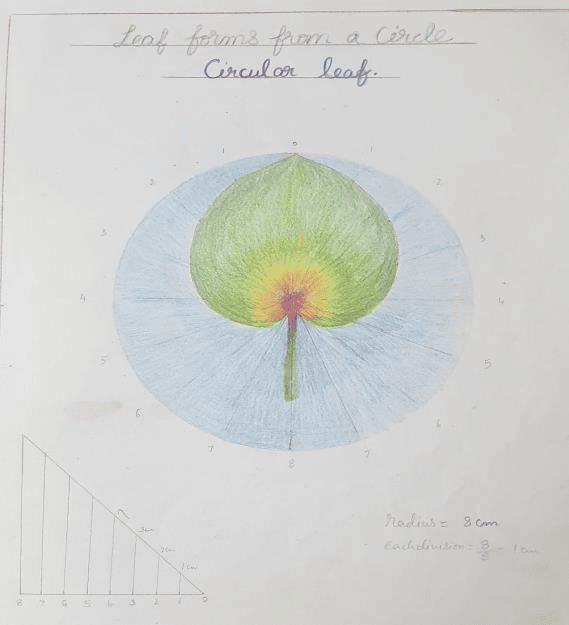
Eighth graders are filled with ideals and opinions; they offer unsolicited judgments and are eager for opportunities to test their powers. Eighth graders undertake a comprehensive review of all mathematical study to date. Understanding the Fibonacci number sequences and the Golden Mean leads students to understand the significance of these ratios in art and architecture. The study of geometry moves to the three-dimensional. The class constructs the Platonic solids —the cube, tetrahedron, octahedron, icosahedrons, and dodecahedron.


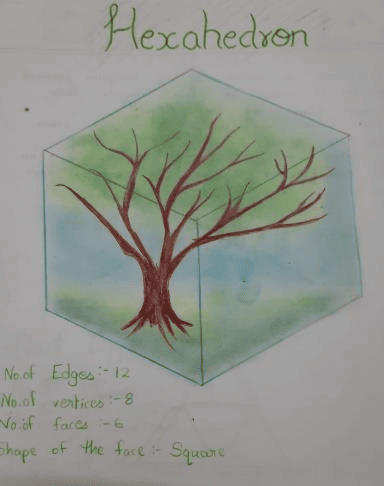
Throughout these stages, various learning modes complement mathematical instruction, such as drawing geometric shapes and experimenting with folded paper. Artistic projects serve as a conduit for a deeper understanding of mathematics. Concepts like balance and symmetry come to life as students draw triangles within triangles, accompanied by storytelling that identifies patterns in both the geometric drawings and their surroundings.
In the Waldorf classroom, the integration of diverse learning modalities facilitates the simultaneous engagement of the left and right brain hemispheres. This approach not only imparts knowledge but also cultivates a holistic perspective. Students explore the historical figures behind mathematical concepts, such as Aryabhata’s introduction of zero in the decimal system, the Pythagorean theorem by the Greeks, and the contributions of Muhammad ibn Musa al-Khwarizmi, known as the “father of algebra.”
By learning about the origins, history, practical applications, and artistic representations of mathematical concepts, Waldorf students develop a comprehensive awareness. This approach fosters a deep-rooted understanding and shapes their perspective by revealing the interconnectedness of subjects. This pedagogical approach aims not only to offer an enriching educational experience but also to inspire students to become well-rounded individuals who perceive connections across different cultures, communities, and the natural world. Through this methodology, Waldorf Education strives to nurture students who possess a broader and more compassionate understanding of their place in the global context.

